I remember the times when I searched for measure theory lectures online and got frustrated immediately at the sight of the abstract definition of Borel set, and the times that I could not wrap my head around when I studied the outer measure in the probability class. Now I may share some points that have helped me understand the concepts of \(\sigma\)-field, outer measure and Lebesgue measure. Rigorous definitions are omitted as there are abundant resources available online, only general ideas are discussed in the post.

1. Notations

Let sample space \(\Omega\) be the unit interval \((0,1]\), a subinterval \(I\) of \(\Omega\) has the form \(I=(a,b]\) where \(0<a\leq b\leq1\), then \(\mu(I)=b-a\) is ordinary length.

Let \(F\) be the class of sets that are disjoint unions of subintervals of \(\Omega\), then it can be shown that \(F\) is a filed. If a set \(A\in F\) then we call \(A\) a \(F\)-set. \(\sigma(F)\) is the \(\sigma\)-field generated by \(F\).

It can be checked that \(\mu\) is a measure on field \(F\).

Let \(\mu^(A)=\inf \sum_{n}\mu(A_n)\), where the infimum extends over all finite and countable coverings of \(A\) by \(F\)-sets \(A_n\). \(\mu^\) is an outer measure.

The triple \((\Omega, \sigma(F), \mu^*|_{\sigma(F)})\) is a measure space that one would often encounter in the probability problem settings, where \( \mu^{*}|_{\sigma(F)}\) is the outer measure restricted on \(\sigma(F)\). Generally, the measure space is usually written as \((\Omega, \mathcal{F}, P)\), where \(\mathcal{F}\) is a \(\sigma\)-field and \(P\) is a measure on \(\mathcal{F}\).

2. Why we need \(\sigma\)-field?

As indicated by the composition of the measure space, we cannot talk about \(\sigma\)-field without mentioning the sample space or the measure. Here is a great post discussing why we need a \(\sigma\)-field other than other class of sets in the measure space. The basic idea is that when the sample space \(\Omega\) is uncountable such as \((0,1]\), it’s not possible to assign probability to every one of the \(2^{\Omega}\) subsets of \(\Omega\), for example, the Vitali set (V) which has been shown to have \(\mu(V)=0\) and \(\mu(V)=1\) at the same time, the contradiction makes it not measurable by \(\mu\). So it’s necessary to work within subclasses of the power class (the class of all subsets of a space), and \(\sigma\)-field is an appropriate subclass whose properties (closure under countable unions and complement) filters out those sets with pathological behaviors.

Besides, probability problem usually starts with the sets of some rather small class \(F\), the finite and countable operations can then lead to sets outside the initial class \(F\). This makes one to consider a class of sets that (i) contains \(F\) and (ii) is a \(\sigma\)-field (which filters out the non-measurable sets), in addition (iii) is as small as possible in a certain sense. As it turns out, this class is the intersection of all the \(\sigma\)-fields containing \(F\), which is \(\sigma(F)\).

3. What does the outer measure do?

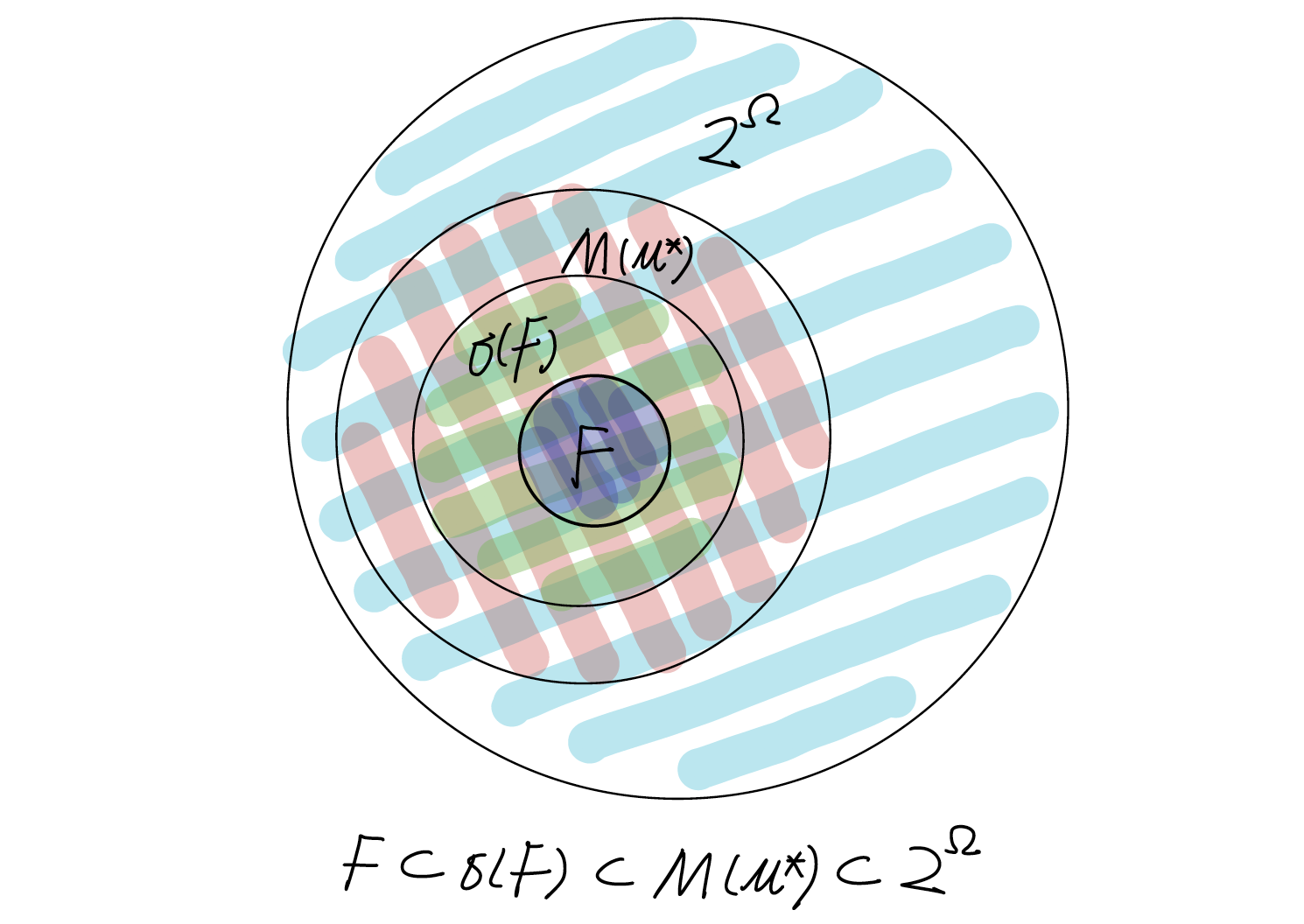
Start from a measure \(\mu\) on a field \(F\), we need to obtain a measure on \(\sigma(F)\) in order to construct the measure space. There are four classes of sets involved in the process: \(F, \sigma(F), M(\mu^{*})\) and \(2^{\Omega} \), where \(M(\mu^{*})\) is the class of set \(A\) satisfying \(\mu^{*}(E\cap A) + \mu^{*}(E\cap A^c) = \mu^{*}(E)\) for every set \(E\subset\Omega\), and it’s a \(\sigma\)-field. The figure below explains the relationship among those classes is that \(F\subset \sigma(F) \subset M(\mu^{*}) \subset 2^{\Omega} \).

Once we have the classes, the measure on \(\sigma(F)\) can be obtained from the outer measure \(\mu^{*}\). \(\mu^{*}\) is a measure defined on the power set \(2^{\Omega}\), and it can be proved that \(\mu^{*}\) restricted on \(M(\mu^{*})\) is a measure there, and then \(\mu^{*}\) further restricted to \(\sigma(F)\) is clearly a measure on that class as well. Therefore the measure space is obtained as \((\Omega, \sigma(F), \mu^*|_{\sigma(F)})\).

4. Lebesgue measure on unit interval

As mentioned in section 1, the space \(\Omega\) is the unit interval \((0,1]\); \(F\) is the class of sets that are disjoint unions of subintervals of \(\Omega\); \(\sigma(F)\) is the \(\sigma\)-field generated by \(F\), which is also often referred as the Borel sets on unit interval; measure \(\mu\) on \(F\) is the ordinary length. Following the strategy elaborated in section 3, we can obtain the measure space \(((0,1], \sigma(F), \mu^{*}|_{\sigma(F)})\), where \(\mu^{*}|_{\sigma(F)}\) is the Lebesgue measure on unit interval.