I was having a hard time understanding the slicing along different axes of a 3d-array in python. Since the best way to learn is through practice, here I will list some helpful examples that has enhanced my understanding, and an application on converting a colorful image to a grayscale image. I will use functions numpy.apply_along_axis and numpy.apply_over_axes to illustrate the ideas, their operations look confusing at the first sight, but once you understand the difference, you will certainly have a better perception about the topic.

# import libraries
import numpy as np
import matplotlib.pyplot as plt

We start from a 2d-array A of shape (2,3). When we slice along an axis, for example, row axis(axis=0), the slices are the columns. More specifically, slices are A[:,0], A[:,1], A[:,2]. Each A[:,j] is a 1d-array by looping over (slice along) the row indices when column index is fixed.

A = np.arange(0,3).reshape((1,3))
A = np.repeat(A, repeats=2, axis=0)
print('2d-arry A is\n',A,'\n')

print('apply mean function along the row axis(axis=0)')
print(np.apply_along_axis(np.mean, 0, A))

2d-arry A is
 [[0 1 2]
 [0 1 2]] 

apply mean function along the row axis(axis=0)
[0. 1. 2.]

Next we look at a 3d-array example. B is of shape (2,4,3). When we slice along an axis, for example, the last axis(axis=-1 or axis=2), the slices are B[i,j,:] (i=0,1, j=0,1,2,3). Each B[i,j,:] is a 1d-array by looping over (slice along) the last axis indices when the first two axes indices are fixed. Suppose we apply a np.mean along the last axis, we will get a 2d-array of shape (2,4), the (0,0)th element of which is np.mean(B[0,0,:])=np.mean([0,40,80])=40, the (1,0)th element of which is np.mean(B[1,0,:])=np.mean([120,160,200])=160.

# create a 3d-arrary of shape (2,4,3)
B = np.arange(0,240,40).reshape((2,3))
B = np.repeat(B, repeats=4, axis=0)
B = B.reshape((2,4,3))
print('3d-arry B is\n',B,'\n')

print('apply mean function along the last axis(axis=-1)')
print(np.apply_along_axis(np.mean, -1, B))

3d-arry B is
 [[[  0  40  80]
  [  0  40  80]
  [  0  40  80]
  [  0  40  80]]

 [[120 160 200]
  [120 160 200]
  [120 160 200]
  [120 160 200]]] 

apply mean function along the last axis(axis=-1)
[[ 40.  40.  40.  40.]
 [160. 160. 160. 160.]]

Here is an application where we use slices along certain axis of a 3d-array data.

Colorful image is often a 3d-array with the last axis indicating the three RGB channels. One way to turn the color to grayscale is to average the 3d-array values over the last axis(color channels), then populate the mean values along the last axis such that each color channel has the same values. We first define a function that calculates and populates the mean along the last axis, then plot the pictures before and after the transformation.

# function to_gray
def to_gray(x, axis=-1, repeats=3):
  return np.apply_along_axis(lambda y: np.repeat(np.mean(y),repeats=3), 
                             # repeat the mean 3 times because there are 3 color channels
                             axis=-1, # function apply along the last axis
                             x)

B_scale = B/255.0 # scale the value to be in [0,1]
figs, axes = plt.subplots(1,2)

axes[0].imshow(B_scale)
axes[0].set_title("Original")
axes[0].axis('Off')

axes[1].imshow(to_gray(B_scale))
axes[1].set_title("Transformed")
axes[1].axis('Off')
plt.show()

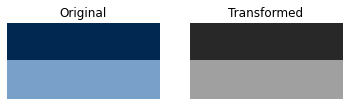
Another function I want to present is numpy.apply_over_axes, it applies a function repeatedly over multiple axes. The difference from numpy.apply_along_axis is that apply_along_axis applies function on each 1d-array slice, but the apply_over_axes applies function on each multi-dimension array slice.

Use B as an exmaple, np.apply_along_axis(np.mean, -1, B) applies mean function on each 1d-array B[i,j,:] slice, since indices vary over (i,j) we get a output of shape (2,4); np.apply_over_axis(np.mean, B, [0,1]) applies mean function on each 2d-arry B[:,:,k], since index varies over k, we get a output of shape (,,3).

print('apply mean function over the first two axes(axes=[0,1])')
print(np.apply_over_axes(np.mean, B, [0,1]))

print('\nmean over 2d-array B[:,:,0]')
print(np.mean(B[:,:,0]))

print('\nmean over 2d-array B[:,:,1]')
print(np.mean(B[:,:,1]))

print('\nmean over 2d-array B[:,:,2]')
print(np.mean(B[:,:,2]))

apply mean function over the first two axes(axes=[0,1])
[[[ 60. 100. 140.]]]

mean over 2d-array B[:,:,0]
60.0

mean over 2d-array B[:,:,1]
100.0

mean over 2d-array B[:,:,2]
140.0